Paseo-por-arboles-de-Madrid/paseo_static_text_sp.md

Introducción

Paseo por los árboles de Madrid es un libro en la Editorial Algoliteraria: crear alianzas con los árboles.
El autor de este libro es el algoritmo de las cadenas de Markov. Genera simultáneamente un poema y un paseo por los árboles del barrio de Las Letras, en el centro de Madrid.
El poema se crea a partir de una novela elegida por el lector. Éste tiene la opción entre dos novelas de grandes escritores españoles del siglo 19:

• La madre naturaleza de la escritora feminista Emilia Pardo Bazán publicada en 1887. Usa en esta obra una prosa poética y descriptiva, y en sus páginas se siente el amor que profesa al paisaje gallego, con un conocimiento de la botánica y de las costumbres rurales muy superior al de sus contemporáneos.
• Miau del escritor Benito Pérez Galdós publicada en 1888. Enmarcada en el género realista, satiriza el Madrid burocrático de finales del siglo XIX a partir de las vicisitudes vitales de su protagonista, Ramón Villaamil, un competente exempleado del Ministerio de Hacienda, al que una serie de intrigas han dejado cesante.

El paseo se genera a partir de la base de datos con árboles en Madrid, Un Alcorque, un Árbol. Cada palabra significativa - sustantivo, adjetivo, verbo o adverbio - está relacionada a un árbol en el Barrio de las Letras de Madrid. Las otras palabras crean el camino entre los diferentes árboles. Así se puede ir caminando por el barrio recitando partes del poema a cada árbol que se encuentra en el paseo.
Este libro es por definición infinito y único.
Está creada por Anaïs Berck. Es un seudónimo que representa una colaboración entre humanos, algoritmos y árboles. Anaïs Berck explora las especificidades de la inteligencia humana en compañía de las inteligencias artificiales y vegetales.
La Editorial Algoliteraria es una colección de publicaciones en las cuales los algoritmos son los autores de libros inusuales. Este libro fue creado como parte de una residencia en el centro de arte contemporáneo Medialab Prado en Madrid. La residencia fue concedida por el programa "Residencia Cultura Digital" iniciado por el Gobierno Flamenco.

En esta obra Anaïs Berck está representadx por:

• el algoritmo de las cadenas de Markov del cual se encuentra una descripción en este libro,
• los árboles de Madrid, que tienen su geolocalización entre Medialab Prado, Plaza del Sol y Atocha Renfe, dentro de la base de datos Un Alcorque, un Árbol,
• los seres humanos Emilia Pardo Bazán, Benito Pérez Gáldos, Jaime Munárriz, Luis Morell, An Mertens, Eva Marina Gracia, Gijs de Heij, Ana Isabel Garrido Mártinez, Alfredo Calosci, Daniel Arribas Hedo.

Poema & Paseo

Descripción general de las cadenas de Markov

Fuentes

https://spectrum.ieee.org/andrey-markov-and-claude-shannon-built-the-first-language-generation-models http://langvillea.people.cofc.edu/MCapps7.pdf https://www.irishtimes.com/news/science/that-s-maths-andrey-markov-s-brilliant-ideas-are-still-bearing-fruit-1.3220929 http://www.alpha60.de/research/markov/DavidLink_TracesOfTheMouth_2006.pdf

Historias

Andrey Andreyevich Markov fue un matemático ruso que vivió entre 1856 y 1922. Sus estudios más famosos fueron con las cadenas de Markov, un algoritmo que permite predecir los cambios futuros una vez que se conoce el estado actual. El primer trabajo sobre el tema se publicó en 1906. También se interesó por la literatura. Intentó establecer un modelo matemático lingüístico mediante cadenas de Markov contando manualmente las letras de la novela en verso de Alexander Pusjkin, Eugene Onegin. A continuación, aplicó el método a la novela Años de infancia del nieto de Bagrov, de S.T. Aksakov. Esto vincula las cadenas de Markov directamente con el campo de la literatura, el texto y el lenguaje. Y el vínculo vivirá firmemente a lo largo de la historia de este algoritmo.

El siguiente texto se basa en el artículo de Oscar Schwartz para IEEE Spectrum, Andrey Markov & Claude Shannon Counted Letters to Build the First Language-Generation Models.
En 1913, Andrey Markov se sentó en su estudio de San Petersburgo con un ejemplar de la novela en verso del siglo XIX de Alexander Pushkin, Eugene Onegin, un clásico literario de la época. Esta obra consta de casi 400 estrofas de tetrámetro yámbico. Sin embargo, Markov no se puso a leer el famoso texto de Pushkin. Más bien, tomó un bolígrafo y un trozo de papel, y escribió las primeras 20.000 letras del libro en una larga cadena de letras, eliminando todos los signos de puntuación y los espacios. A continuación, dispuso estas letras en 200 cuadrículas (de 10 por 10 caracteres cada una) y comenzó a contar las vocales en cada fila y columna, contabilizando los resultados.
Al separar las vocales de las consonantes, Markov ponía a prueba una teoría de la probabilidad que había desarrollado en 1906 y que ahora llamamos Proceso de Markov o Cadena de Markov. Hasta ese momento, el campo de la probabilidad se había limitado principalmente a analizar fenómenos como la ruleta o el lanzamiento de una moneda, en los que el resultado de eventos anteriores no cambia la probabilidad de los eventos actuales. Pero Markov pensaba que la mayoría de las cosas ocurren en cadenas de causalidad y dependen de resultados anteriores. Quería una forma de modelar estos sucesos mediante un análisis probabilístico.
Markov creía que el lenguaje era un ejemplo de sistema en el que los sucesos pasados determinan en parte los resultados presentes. Para demostrarlo, quería mostrar que en un texto como la novela de Pushkin, la probabilidad de que una determinada letra aparezca en algún momento del texto depende, hasta cierto punto, de la letra que la precede.
Para ello, Markov comenzó a contar las vocales en Eugene Onegin, y descubrió que el 43% de las letras eran vocales y el 57% consonantes. A continuación, Markov separó las 20.000 letras en pares de combinaciones de vocales y consonantes. Descubrió que había 1.104 pares vocal-vocal, 3.827 pares consonante-consonante y 15.069 pares vocal-consonante y consonante-vocal. Lo que esto demostró, estadísticamente hablando, fue que para cualquier letra del texto de Pushkin, si era una vocal, las probabilidades eran que la siguiente letra fuera una consonante, y viceversa.
Markov utilizó este análisis para demostrar que Eugene Onegin de Pushkin no era sólo una distribución aleatoria de letras, sino que tenía algunas cualidades estadísticas subyacentes que podían modelarse. El enigmático trabajo de investigación que surgió de este estudio, titulado An Example of Statistical Investigation of the Text Eugene Onegin Concerning the Connection of Samples in Chains(Un ejemplo de investigación estadística del texto Eugene Onegin sobre la conexión de muestras en cadenas), no fue muy citado en vida de Markov, y no se tradujo al inglés hasta 2006. Markov se vio obligado a interrumpir sus experimentos de recuento de letras, cuando había perdido casi por completo la vista debido a un glaucoma. Aunque Markov hubiera tenido más tiempo y mejor vista para llevar a cabo sus experimentos, las extensiones habrían sido muy difíciles de completar, dada la época preinformática en la que vivió, en la que los esfuerzos computacionales debían pagarse en años-hombre.

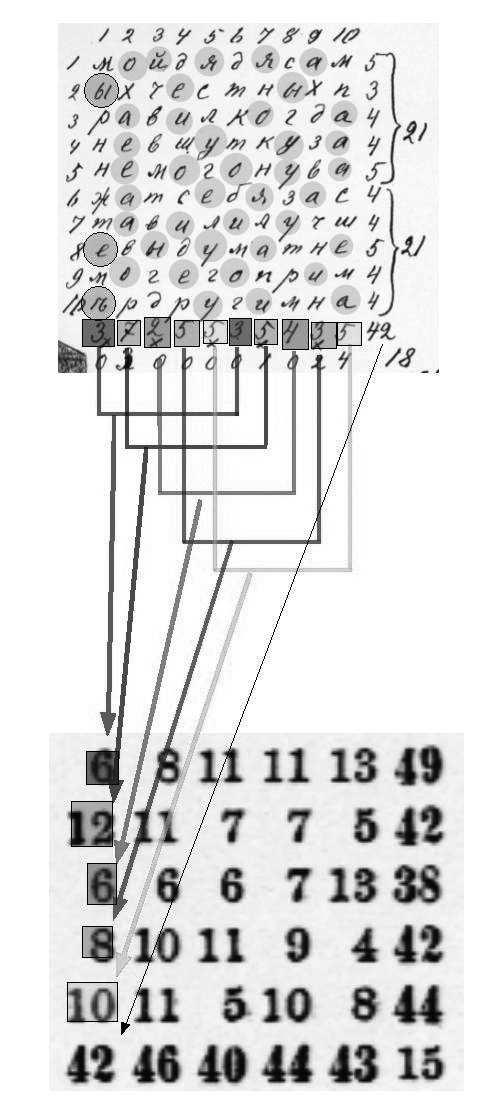
These images show Markov’s original notes in computing the probabilities needed for his Pushkin chain.

Influencia

Algunos de los conceptos centrales de Markov en torno a la probabilidad y el lenguaje se extendieron por el mundo entero, y acabaron encontrando su rearticulación en el enormemente influyente documento de Claude Shannon, A Mathematical Theory of Communication, que se publicó en 1948.
El documento de Shannon esbozaba una forma de medir con precisión la cantidad de información en un mensaje y, al hacerlo, sentaba las bases de una teoría de la información que llegaría a definir la era digital. A Shannon le fascinaba la idea de Markov de que, en un texto dado, se podía aproximar la probabilidad de que apareciera alguna letra o palabra. Al igual que Markov, Shannon lo demostró realizando algunos experimentos textuales (en inglés) que implicaban la elaboración de un modelo estadístico del lenguaje, y luego dio un paso más al tratar de utilizar el modelo para generar texto de acuerdo con esas reglas estadísticas.
En un primer experimento de control, empezó generando una frase eligiendo letras al azar de un alfabeto de 27 símbolos (26 letras, más un espacio), y obtuvo el siguiente resultado:

XFOML RXKHRJFFJUJ ZLPWCFWKCYJ FFJEYVKCQSGHYD QPAAMKBZAACIBZLHJQD

La frase era ruido sin sentido, dijo Shannon, porque cuando nos comunicamos no elegimos las letras con igual probabilidad. Como había demostrado Markov, las consonantes son más probables que las vocales. Pero a un mayor nivel de granularidad, las E son más comunes que las S, que son más comunes que las Q. Para tener en cuenta este hecho, Shannon modificó su alfabeto original para que se ajustara más a la probabilidad del inglés: era un 11% más probable sacar una E del alfabeto que una Q. Cuando volvió a sacar letras al azar de este corpus recalibrado, obtuvo una frase que se acercaba un poco más al inglés.

OCRO HLI RGWR NMIELWIS EU LL NBNESEBYA TH EEI ALHENHTTPA OOBTTVA NAH BRL.

In a series of subsequent experiments, Shannon demonstrated that as you make the statistical model even more complex, you get increasingly more comprehensible results. Shannon, via Markov, revealed a statistical framework for the English language, and showed that by modeling this framework—by analyzing the dependent probabilities of letters and words appearing in combination with each other—he could actually generate language.

Cuanto más complejo sea el modelo estadístico de un texto dado, más precisa será la generación del lenguaje, o como dijo Shannon, mayor será el "parecido con el texto inglés ordinario". En el experimento final, Shannon recurrió a un corpus de palabras en lugar de letras y consiguió lo siguiente:

THE HEAD AND IN FRONTAL ATTACK ON AN ENGLISH WRITER THAT THE CHARACTER OF THIS POINT IS THEREFORE ANOTHER METHOD FOR THE LETTERS THAT THE TIME OF WHO EVER TOLD THE PROBLEM FOR AN UNEXPECTED.

Tanto para Shannon como para Markov, la idea de que las propiedades estadísticas del lenguaje podían ser modeladas ofrecía una forma de replantear problemas más amplios en los que estaban trabajando. Para Markov, amplió el estudio de la estocasticidad más allá de los eventos mutuamente independientes, abriendo el camino para una nueva era en la teoría de la probabilidad. Para Shannon, le ayudó a formular una forma precisa de medir y codificar unidades de información en un mensaje, lo que revolucionó las telecomunicaciones y, finalmente, la comunicación digital. Pero su enfoque estadístico en la modelación y la generación del lenguaje también marcó el comienzo de una nueva era para el procesamiento del lenguaje natural, que se ha ramificado en la era digital hasta nuestros días. Como señala David Link en su artículo Traces of the Mouth, los esfuerzos de Markov en retrospectiva "representan un intento temprano y trascendental de entender el fenómeno del lenguaje en términos matemáticos". No es exagerado decir que el análisis de texto de Markov es, en principio, similar a lo que Google y otras empresas llevan a cabo ahora de forma rutinaria y a gran escala: analizar las palabras de los libros y los documentos de Internet, el orden en que aparecen las palabras, analizar las frases de búsqueda, detectar el spam, etc.

Applicaciones

Dado que las cadenas de Markov pueden diseñarse para modelar muchos procesos del mundo real, se utilizan en una gran variedad de situaciones. Aparecen en física y química cuando se utilizan probabilidades para cantidades desconocidas. En el tratamiento de la información, desempeñan un papel en el reconocimiento de patrones, el análisis y la síntesis automática del habla y la compresión de datos. Los meteorólogos, ecologistas y biólogos los utilizan. Otras aplicaciones son el control de coches sin conductor, la traducción automática, los patrones de colas y la predicción del crecimiento de la población, los precios de los activos, los cambios de moneda y las crísis del mercado. También artistas han utilizado las cadenas de Markov, como el músico Iannis Xenakis, que desarrolló la "Música estocástica libre" basada en las cadenas de Markov.

En 2006 - el centenario del artículo de Markov - Philipp Von Hilgers y Amy Langville resumieron las cinco mayores aplicaciones de las cadenas de Markov. Entre ellas se encuentra la que utilizamos la mayoría de nosotros a diario: el Page Rank de Google. Cada vez que buscamos en Internet, la clasificación de las páginas web se basa en una solución de la cadena de Markov masiva. Se puede decir que todas las páginas web son estados, y los enlaces entre ellas son transiciones que poseen probabilidades específicas. En otras palabras, podemos decir que, independientemente de lo que busques en Google, hay una probabilidad finita de que acabes en una página web concreta. Si utilizas Gmail, habrás notado su función de autorrelleno. Esta función predice automáticamente tus frases para ayudarte a escribir correos electrónicos rápidamente. Las cadenas de Markov ayudan considerablemente en este sector, ya que pueden proporcionar predicciones de este tipo de forma eficaz.
Y por último, pero no menos importante, ¿te has preguntado alguna vez por qué el spam tiene todas esas divertidas cadenas de palabras sin sentido? Son construcciones bastante extrañas, no tan aleatorias como si se sacaran palabras al azar de un sombrero, casi gramaticales la mayor parte de las veces, pero aún así son un claro galimatías. También aquí las cadenas de Markov han asumido gran parte del trabajo.

Descripción técnica de las cadenas de Markov

Sources:

https://en.wikipedia.org/wiki/Examples_of_Markov_chains https://higherkindedtripe.wordpress.com/2012/02/26/markov-chains-or-daddy-where-does-spam-come-from/ https://towardsdatascience.com/predicting-the-weather-with-markov-chains-a34735f0c4df

En un proceso de Markov podemos predecir los cambios futuros una vez que conocemos el estado actual. Wikipedia describe muy bien la diferencia entre las cadenas de Markov y otros sistemas: "Un juego de serpientes y escaleras o cualquier otro juego cuyas jugadas se determinan enteramente por los dados es una cadena de Markov, de hecho, una cadena de Markov absorbente. Esto contrasta con los juegos de cartas, como el blackjack, donde las cartas representan una "memoria" de las jugadas anteriores. Para ver la diferencia, considere la probabilidad de un determinado evento en el juego. En los juegos de dados mencionados, lo único que importa es el estado actual del tablero. El siguiente estado del tablero depende del estado actual y de la siguiente tirada de dados. No depende de cómo han llegado las cosas a su estado actual. En un juego como el blackjack, un jugador puede obtener ventaja recordando qué cartas se han mostrado ya (y, por tanto, qué cartas ya no están en la baraja), por lo que el siguiente estado (o mano) del juego no es independiente de los estados pasados". Así, para un proceso de Markov, sólo el estado actual determina el siguiente estado; la historia del sistema no tiene ningún impacto. Por eso describimos un proceso de Markov como sin memoria. Lo que ocurre a continuación viene determinado completamente por el estado actual y las probabilidades de transición.
A continuación, describimos un funcionamiento clásico de las cadenas de Markov, junto a una versión simplificada que hemos utilizado para desarrollar un juego de Markov y el código de este libro.

Versión clásica

Este ejemplo está tomado de la siguiente fuente: https://higherkindedtripe.wordpress.com/2012/02/26/markov-chains-or-daddy-where-does-spam-come-from/

Coge un texto de "entrenamiento".
Haz una lista de todas las palabras que contiene.
Para cada palabra, haga una lista de todas las demás palabras que vienen después de ella, con el número de veces que aparece cada palabra. Así, con la frase "the quick brown fox jumped over the lazy dog", acabarías con la lista:

1. the -> (1, quick), (1, lazy)
2. quick -> (1, brown)
3. brown -> (1, fox)
4. fox -> (1, jumped)
5. jumped -> (1, over)
6. over -> (1, the)
7. lazy -> (1, dog)
8. dog ->

Convierte la lista en una matriz, en la que las filas representan las palabras "principales" y las columnas representan las palabras "siguientes", y cada número de la matriz dice cuántas veces apareció la palabra siguiente después de la palabra principal. Obtendrás:

	the	quick	brown	fox	jumped	over	lazy	dog
the	0	1	0	0	0	0	1	0
quick	0	0	1	0	0	0	0	0
brown	0	0	0	1	0	0	0	0
fox	0	0	0	0	1	0	0	0
jumped	0	0	0	0	0	1	0	0
over	0	0	0	0	0	0	1	0
lazy	0	0	0	0	0	0	0	1
dog	0	0	0	0	0	0	0	0

Divide cada número de la matriz por el total de su fila y verás que cada fila se convierte en una especie de distribución de probabilidad.

	the	quick	brown	fox	jumped	over	lazy	dog
the	0	0.5	0	0	0	0	0.5	0
quick	0	0	1	0	0	0	0	0
brown	0	0	0	1	0	0	0	0
fox	0	0	0	0	1	0	0	0
jumped	0	0	0	0	0	1	0	0
over	0	0	0	0	0	0	1	0
lazy	0	0	0	0	0	0	0	1
dog	0	0	0	0	0	0	0	0

Se puede interpretar como que "si la primera palabra es un 'the', hay un 50% de posibilidades de que la siguiente palabra sea 'quick', y un 50% de posibilidades de que la siguiente palabra sea 'lazy'. Para todas las demás palabras, sólo hay una palabra posible a continuación".
Casi todas las palabras tienen sólo una posible palabra siguiente porque el texto es muy corto. Pero si se entrena con un texto más extenso y se interpretan las filas como una distribución de probabilidades, se puede empezar a ver para cada palabra qué tipo de palabra tiende a seguirla. Esto ofrece una visión muy interesante del carácter del texto escrito.
Si tomas esa gran "matriz de transición" que has entrenado a partir de un texto grande, puedes usarla para generar realmente un nuevo texto de la siguiente manera:

1. Elija al azar una palabra "semilla" del texto. Para obtener los mejores resultados, utilice una con muchas palabras siguientes posibles.

2. Encuentre la fila de la matriz correspondiente a esa palabra. Elija la siguiente palabra al azar, ponderada según las probabilidades de la fila. Es decir, si la columna correspondiente a la palabra "azul" tiene el número 0,05, tienes un 5% de posibilidades de elegir "azul" como siguiente palabra, y así sucesivamente (al dividir cada número por el total de su fila nos aseguramos de que estas probabilidades sumen 1).

3. Vuelve al paso 2 utilizando esta segunda palabra como la nueva palabra "semilla". Continúe este proceso para generar una cadena de palabras tan larga como desee. Si acaba con una palabra a la que no le siguen otras (algo poco común cuando se entrena con una prueba grande, pero posible: imagine que la última palabra de una novela fuera la única ocurrencia de la palabra "xilófono", o lo que sea), simplemente elija una palabra al azar.

Se puede ver cómo las cadenas de palabras generadas con este método seguirán las "tendencias" de los datos de entrenamiento, lo que significa que si se generara una nueva matriz de transición a partir de las palabras generadas, ésta tendría, en promedio, el mismo aspecto que la matriz de transición original, ya que se eligieron las palabras de acuerdo con esos pesos. Este proceso completamente mecánico puede generar datos que se parecen, estadísticamente, a un idioma significativo. Por supuesto, no es necesariamente gramatical, y está ciertamente desprovisto de significado superior, ya que fue generado a través de este proceso simplista.
Esas "cadenas" de palabras construidas por el proceso anterior son un ejemplo de cadenas de Markov. Y también son la respuesta a la pregunta "¿de dónde viene el spam?". Esas divagaciones casi gramaticales debajo de los anuncios de "Viagra", generadas mediante el proceso anterior, son la forma que tienen los creadores de spam de engañar a su filtro de spam. Incluyen estas cadenas para dar a sus anuncios una similitud estadística con la correspondencia humana significativa. Esto funciona porque los filtros de spam utilizan (al menos en parte) modelos probabilísticos que dependen de las transiciones y frecuencias de las palabras para clasificar el correo electrónico entrante como spam. Los emisores de spam y los redactores de los filtros se enzarzan en un eterno juego del gato y el ratón generado aleatoriamente.

Versión simplificada

Con Algolit, un grupo de investigación artística sobre código y literatura libres con sede en Bruselas, desarrollamos un juego de cadenas de Markov con frases y cartas. Esto ocurrió como parte del festival Désert Numérique, en La Drôme en Francia en 2014. El juego fue desarrollado por Brendan Howell, Catherine Lenoble y An Mertens. Puedes escuchar el programa de radio: http://desert.numerique.free.fr//archives/?id=1011&ln=fr.
A continuación, el juego se presentó en Transmediale, en Berlín, en 2015, respetando las siguientes reglas.

1. Tomamos un texto, por ejemplo:

Cqrrelations read as poetry to statisticians. Can statisticians read poetry with machines? Cqrrelations is a practise for artists, for datatravellers, statisticians and other lovers of machines to explore a world of blurry categorisations and crummylations. Machines correlate to dissidents, dissidents correlate to statisticians.

2. Creamos una base de datos para este texto; cada palabra es una entrada y toma la palabra siguiente como valor posible. La entrada de "Cqrrelations" tendrá dos valores:

   1. read
   2. is

3. Una vez creada la base de datos, elegimos una palabra inicial para un nuevo texto, por ejemplo Cqrrelations.

4. Tiramos el dado, los números impares darán "leer" como 2ª palabra de nuestro texto; los números pares darán "es" como 2ª palabra.

5. Volvemos a tirar el dado y elegimos una palabra entre los valores de la palabra elegida. Esto da la siguiente palabra de nuestra frase.

6. Continuamos 5 hasta llegar a una palabra con un punto (.)

7. Podemos repetir la regla 3 hasta la 6 hasta que estemos satisfechos con la cantidad de frases generadas

Basado en el texto de entrada el resultado en Transmediale fue:

A world of blurry categorisations and other lovers of blurry categorisations and other lovers of blurry categorisations and other lovers of machines. Cqrrelations read poetry to dissidents correlate to machines. Lovers of machines to statisticians.”

Código

Créditos

Este libro es una creación de Anaïs Berck para Medialab como parte del programa "Residencia Cultura Digital" iniciado por el Gobierno Flamenco.
En esta obra Anaïs Berck está representadx por:

• el algoritmo de las cadenas de Markov del cual se encuentra una descripción en este libro,
• los árboles de Madrid, que tienen su geolocalización entre Medialab Prado, Plaza del Sol y Atocha Renfe, dentro de la base de datos Un Alcorque, un Árbol,
• los seres humanos Emilia Pardo Bazán, Benito Pérez Gáldos, Jaime Munárriz, Luis Morell, An Mertens, Eva Marina Gracia, Gijs de Heij, Ana Isabel Garrido Mártinez, Alfredo Calosci, Daniel Arribas Hedo.

La copia de este libro es única y el tiraje es por definición infinito.
Esta copia es el número XXX de copias descargadas.
Condiciones colectivas de (re)uso (CC4r), 2021
Copyleft con una diferencia: Se le invita a copiar, distribuir y modificar esta obra bajo los términos de la CC4r.